CS61A-Spring2022
Lab 14: Final Review
起始文件
下载 lab14.zip 。在该压缩包中,你会发现本实验中问题的起始文件,以及 Ok 自动评分器的副本。
这个实验有很多文件。记住要在 lab14.scm 中写 Scheme 问题,在 lab14.lark 中写 BNF 问题,在 lab14.py 中写所有其他问题。
必要的问题
Scheme
Q1: Split
实现 split-at ,它接收一个列表 lst 和一个非负数 n 作为输入,并返回一对 new ,使得 (car new) 是 lst 的前 n 个元素, (cdr new) 是 lst 的其余元素。如果 n 大于 lst 的长度, (car new) 应该是 lst , (cdr new) 应该是 nil 。
scm> (car (split-at '(2 4 6 8 10) 3))
(2 4 6)
scm> (cdr (split-at '(2 4 6 8 10) 3))
(8 10)
(define (split-at lst n)
'YOUR-CODE-HERE
)
使用 Ok 来测试你的代码:
python3 ok -q split-at
Scheme Data Abstraction
Q2: Filter Odd Tree
编写一个函数 filter-odd ,它接收一个 tree 数据抽象,并返回一个新的 tree ,所有的偶数 label 都被替换为 nil 。
考虑使用
map过程将一个单参数函数应用于一个列表。
下面是本学期我们一直在使用的 Tree 类的 Scheme-ified 数据抽象。
; Constructs tree given label and list of branches
(tree label branches)
; Returns the label of the tree
(label t)
; Returns the list of branches of the given tree
(branches t)
(define (filter-odd t)
'YOUR-CODE-HERE
)
使用 Ok 来测试你的代码:
python3 ok -q filter_odd
Programs as Data
Q3: Swap
实现 swap ,它接收一个表达式 expr ,代表对某个过程的调用,如果第二个操作数的值大于第一个操作数的值,则返回相同的表达式,并将其前两个操作数对换。否则,它应该只返回原始表达式。例如, (swap '(- 1 (+ 3 5) 7)) 应该返回表达式 (- (+ 3 5) 1 7) ,因为 1 的值是 1 , (+ 3 5) 的值是 8 ,而且 8 > 1 。在执行过程中,前两个操作数之后的任何操作数都不应该被计算,它们应该在最后的表达式中保持不变。你可以假设每个操作数都为一个数字,并且在 expr 中总是有至少两个操作数。你可以考虑在提供的程序之外使用 let 表达式来帮助简化你的代码。
(define (cddr s)
(cdr (cdr s))
)
(define (cadr s)
(car (cdr s))
)
(define (caddr s)
(car (cddr s))
)
(define (swap expr)
'YOUR-CODE-HERE
)
使用 Ok 来测试你的代码:
python3 ok -q swap
Regex
Q4: Address First Line
编写一个正则表达式,解析字符串并返回它是否包含美国邮寄地址的第一行。
美国的邮寄地址通常包含一个街区号码,这是一个由 3-5 位数字组成的序列,后面是一个街道名称。街道名称可以由多个单词组成,但总是以街道类型的缩写结束,其本身是一个由 2-5 个英文字母组成的序列。街道名称也可以选择以红线方向(“N”、“E”、“W”、“S”)开始。一切都应适当地大写。
正确的大写意味着每个名字的第一个字母都是大写的。像 “WeirdCApitalization”这样的匹配是可以的。
参见 doctests 中的一些例子。
def address_oneline(text):
"""
Finds and returns if there are expressions in text that represent the first line
of a US mailing address.
>>> address_oneline("110 Sproul Hall, Berkeley, CA 94720")
True
>>> address_oneline("What's at 39177 Farwell Dr? Is there a 39177 Nearwell Dr?")
True
>>> address_oneline("I just landed at 780 N McDonnell Rd, and I need to get to 1880-ish University Avenue. Help!")
True
>>> address_oneline("123 Le Roy Ave")
True
>>> address_oneline("110 Unabbreviated Boulevard")
False
>>> address_oneline("790 lowercase St")
False
"""
block_number = r'___'
cardinal_dir = r'___' # whitespace is important!
street = r'___'
type_abbr = r'___'
street_name = f"{cardinal_dir}{street}{type_abbr}"
return bool(re.search(f"{block_number} {street_name}", text))
使用 Ok 来测试你的代码:
python3 ok -q address_oneline
BNF
Q5: WWPD: PyCombinator
考虑一下这个用于 Pycombinator 的 BNF 语法的尝试,这个语法支持 Python 的一个子集的功能。具体来说,它能够解析任何带有 Python 算术运算符的表达式。该语法的具体内容如下:
?start: pycomb_expression
pycomb_expression: func "(" arg ("," arg)* ")"
arg: pycomb_expression | NUMBER
func: FUNCNAME
FUNCNAME: "add" | "mul" | "sub"
%ignore " "
%import common.NUMBER
让我们通过几个问题来了解和修改这个 BNF 的功能。
使用 Ok 来测试你对知识的理解,为以下每个“PyCombinator会做什么”的问题选择最佳答案:
python3 ok -q wwpd-bnf -u
提交
请确保提交该实验:
python3 ok --submit
推荐问题
以下问题不是本实验的学分要求,但可以帮助你为期末考试做准备。
Trees
Q6: Prune Min
编写一个函数,对一棵 Tree t 进行修剪, t 及其分支总是有零或两个分支。对于有两个分支的树,通过保留具有较小标签值的分支,将分支的数量从两个减少到一个。对零分支的树不做任何处理。
按照你选择的方向(自上而下或自下而上)对树进行修剪。结果应该是一棵线性树。
def prune_min(t):
"""Prune the tree mutatively.
>>> t1 = Tree(6)
>>> prune_min(t1)
>>> t1
Tree(6)
>>> t2 = Tree(6, [Tree(3), Tree(4)])
>>> prune_min(t2)
>>> t2
Tree(6, [Tree(3)])
>>> t3 = Tree(6, [Tree(3, [Tree(1), Tree(2)]), Tree(5, [Tree(3), Tree(4)])])
>>> prune_min(t3)
>>> t3
Tree(6, [Tree(3, [Tree(1)])])
"""
"*** YOUR CODE HERE ***"
使用 Ok 来测试你的代码:
python3 ok -q prune_min
Q7: Add trees
定义函数 add_trees ,它接收两棵树并返回一棵新的树,其中第一棵树的每个对应节点都被添加到第二棵树的节点中。如果某个位置的节点出现在一棵树上,但没有出现在另一棵树上,那么它也应该出现在新树上。
提示: 你可能想使用内置的 zip 函数来一次迭代多个序列。
def add_trees(t1, t2):
"""
>>> numbers = Tree(1,
... [Tree(2,
... [Tree(3),
... Tree(4)]),
... Tree(5,
... [Tree(6,
... [Tree(7)]),
... Tree(8)])])
>>> print(add_trees(numbers, numbers))
2
4
6
8
10
12
14
16
>>> print(add_trees(Tree(2), Tree(3, [Tree(4), Tree(5)])))
5
4
5
>>> print(add_trees(Tree(2, [Tree(3)]), Tree(2, [Tree(3), Tree(4)])))
4
6
4
>>> print(add_trees(Tree(2, [Tree(3, [Tree(4), Tree(5)])]), \
Tree(2, [Tree(3, [Tree(4)]), Tree(5)])))
4
6
8
5
5
"""
"*** YOUR CODE HERE ***"
使用 Ok 来测试你的代码:
python3 ok -q add_trees
Objects
让我们来实现一个名为选举的游戏。在这个游戏中,两个玩家竞争,试图赢得最多的选票。两个玩家都从 0 票和 100 人气开始。
两个玩家交替轮流,由第一个玩家开始。每一回合,当前玩家选择一个行动。有两种类型的行动:
- 玩家可以进行辩论,并获得或失去 50 个人气。如果玩家的人气为
p1,另一玩家的人气为p2,那么玩家获得 50 人气的概率为max(0.1, p1 / (p1 + p2))注意,max导致概率永远不会低于 0.1 。 - 该玩家可以发表演讲。如果该玩家的人气为
p1,而另一玩家的人气为p2,则该玩家获得p1 // 10票和人气,另一玩家失去p2 // 10人气。
当一个玩家的票数达到 50 票,或者总共进行了 10 个回合(每个玩家进行了 5 个回合)之后,游戏就会结束。游戏结束时,谁的票数多,谁就是赢家!
Q8: Player
首先,我们来实现 Player 类。填写 debate 和 speech 的方法,这些方法接收了另一个 Player other ,并实现了上面详述的正确行为。这里有两件额外的事情要记住:
- 在
debate方法中,你应该调用所提供的random函数,该函数返回一个介于 0 和 1 之间的随机浮点数。如果该随机数小于上述的概率,玩家应该获得 50 的人气,否则会失去 50 的人气。 - 两个玩家的人气都不应该变成负数。如果发生这种情况,就把它改为等于 0 。
### Phase 1: The Player Class
class Player:
"""
>>> random = make_test_random()
>>> p1 = Player('Hill')
>>> p2 = Player('Don')
>>> p1.popularity
100
>>> p1.debate(p2) # random() should return 0.0
>>> p1.popularity
150
>>> p2.popularity
100
>>> p2.votes
0
>>> p2.speech(p1)
>>> p2.votes
10
>>> p2.popularity
110
>>> p1.popularity
135
"""
def __init__(self, name):
self.name = name
self.votes = 0
self.popularity = 100
def debate(self, other):
"*** YOUR CODE HERE ***"
def speech(self, other):
"*** YOUR CODE HERE ***"
def choose(self, other):
return self.speech
使用 Ok 来测试你的代码:
python3 ok -q Player
Q9: Game
现在,实现 Game 类。填写 play 方法,它应该在两个玩家之间交替进行,从 p1 开始,让每个玩家一次轮到一个。 Player 类中的 choose 方法返回应被调用的方法,可以是 debate ,也可以是 speech ,以执行该动作。
此外,填写 winner 方法,它应该返回拥有更多选票的玩家,如果玩家打成平手,则返回 None 。
### Phase 2: The Game Class
class Game:
"""
>>> p1, p2 = Player('Hill'), Player('Don')
>>> g = Game(p1, p2)
>>> winner = g.play()
>>> p1 is winner
True
"""
def __init__(self, player1, player2):
self.p1 = player1
self.p2 = player2
self.turn = 0
def play(self):
while not self.game_over():
"*** YOUR CODE HERE ***"
return self.winner()
def game_over(self):
return max(self.p1.votes, self.p2.votes) >= 50 or self.turn >= 10
def winner(self):
"*** YOUR CODE HERE ***"
使用 Ok 来测试你的代码:
python3 ok -q Game
Q10: New Players
Player 类中的 choose 方法很无聊,因为它总是返回 speech 方法。让我们来实现两个继承自 Player 的新类,但有更有趣的 choose 方法。
在 AggressivePlayer 类中实现 choose 方法,如果玩家的人气小于或等于其他玩家 other 的人气,则返回 debate 方法,否则返回 speech 。同时在 CautiousPlayer 类中实现 choose 方法,如果玩家的人气为 0 ,则返回 debate 方法,反之则返回 speech 。
### Phase 3: New Players
class AggressivePlayer(Player):
"""
>>> random = make_test_random()
>>> p1, p2 = AggressivePlayer('Don'), Player('Hill')
>>> g = Game(p1, p2)
>>> winner = g.play()
>>> p1 is winner
True
"""
def choose(self, other):
"*** YOUR CODE HERE ***"
class CautiousPlayer(Player):
"""
>>> random = make_test_random()
>>> p1, p2 = CautiousPlayer('Hill'), AggressivePlayer('Don')
>>> p1.popularity = 0
>>> p1.choose(p2) == p1.debate
True
>>> p1.popularity = 1
>>> p1.choose(p2) == p1.debate
False
"""
def choose(self, other):
"*** YOUR CODE HERE ***"
使用 Ok 来测试你的代码:
python3 ok -q AggressivePlayer
python3 ok -q CautiousPlayer
Lists
Q11: Intersection - Summer 2015 MT1 Q4
实现 intersection(lst_of_lsts) ,它接收一个列表,并返回一个在 lst_of_lsts 的所有列表中出现的独特元素的列表。如果没有数字出现在所有的列表中,则返回空列表。你可以假设 lst_of_lsts 至少包含一个列表。
def intersection(lst_of_lsts):
"""Returns a list of distinct elements that appear in every list in
lst_of_lsts.
>>> lsts1 = [[1, 2, 3], [1, 3, 5]]
>>> intersection(lsts1)
[1, 3]
>>> lsts2 = [[1, 4, 2, 6], [7, 2, 4], [4, 4]]
>>> intersection(lsts2)
[4]
>>> lsts3 = [[1, 2, 3], [4, 5], [7, 8, 9, 10]]
>>> intersection(lsts3) # No number appears in all lists
[]
>>> lsts4 = [[3, 3], [1, 2, 3, 3], [3, 4, 3, 5]]
>>> intersection(lsts4) # Return list of distinct elements
[3]
"""
elements = []
"*** YOUR CODE HERE ***"
return elements
使用 Ok 来测试你的代码:
python3 ok -q intersection
Q12: Deck of cards
编写一个列表,它将创建一副牌,给定一个花色列表 suits 和一个等级列表 ranks 。列表中的每个元素都是一张牌,它由一个形式为 [suit, rank] 的 2 元列表表示。
def deck(suits, ranks):
"""Creates a deck of cards (a list of 2-element lists) with the given
suits and ranks. Each element in the returned list should be of the form
[suit, rank].
>>> deck(['S', 'C'], [1, 2, 3])
[['S', 1], ['S', 2], ['S', 3], ['C', 1], ['C', 2], ['C', 3]]
>>> deck(['S', 'C'], [3, 2, 1])
[['S', 3], ['S', 2], ['S', 1], ['C', 3], ['C', 2], ['C', 1]]
>>> deck([], [3, 2, 1])
[]
>>> deck(['S', 'C'], [])
[]
"""
"*** YOUR CODE HERE ***"
return ______
使用 Ok 来测试你的代码:
python3 ok -q deck
Linked Lists
Q13: O!-Pascal - Fall 2017 Final Q4
帕斯卡尔三角形也许是你熟悉的,下图显示了前五行的情况。
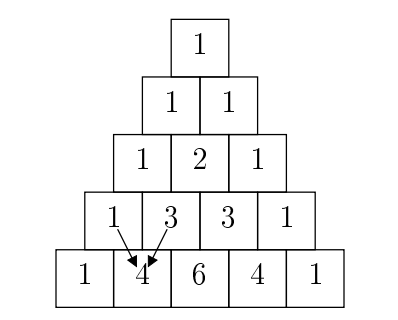
每一个方格都是它上面两个方格的总和(如箭头所示,这里的数值 4 ),除非它上面没有两个方格,在这种情况下,它的数值是 1 。
给出一个代表帕萨尔三角形中某一行的链表,返回一个代表它下面一行的链表。
def pascal_row(s):
"""
>>> a = Link.empty
>>> for _ in range(5):
... a = pascal_row(a)
... print(a)
<1>
<1 1>
<1 2 1>
<1 3 3 1>
<1 4 6 4 1>
"""
"*** YOUR CODE HERE ***"
使用 Ok 来测试你的代码:
python3 ok -q pascal_row