CS61A-Spring2022

Lab 4: Recursion, Tree Recursion

Starter Files

Download lab04.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the Ok autograder.

Topics

Consult this section if you need a refresher on the material for this lab. It’s okay to skip directly to the questions and refer back here should you get stuck.

Recursion

A recursive function is a function that calls itself in its body, either directly or indirectly.

Let’s look at the canonical example, factorial.

Factorial, denoted with the ! operator, is defined as:

n! = n * (n-1) * ... * 1

For example, 5! = 5 * 4 * 3 * 2 * 1 = 120

The recursive implementation for factorial is as follows:

def factorial(n):
    if n == 0:
        return 1
    return n * factorial(n - 1)

We know from its definition that 0! is 1. Since n == 0 is the smallest number we can compute the factorial of, we use it as our base case. The recursive step also follows from the definition of factorial, i.e., n! = n * (n-1)!.

Recursive functions have three important components:

1. Base case. You can think of the base case as the case of the simplest function input, or as the stopping condition for the recursion. In our example, factorial(1) is our base case for the factorial function.
2. Recursive call on a smaller problem. You can think of this step as calling the function on a smaller problem that our current problem depends on. We assume that a recursive call on this smaller problem will give us the expected result; we call this idea the “recursive leap of faith”. In our example, factorial(n) depends on the smaller problem of factorial(n-1).
3. Solve the larger problem. In step 2, we found the result of a smaller problem. We want to now use that result to figure out what the result of our current problem should be, which is what we want to return from our current function call. In our example, we can compute factorial(n) by multiplying the result of our smaller problem factorial(n-1) (which represents (n-1)!) by n (the reasoning being that n! = n * (n-1)!).

The next few questions in lab will have you writing recursive functions. Here are some general tips:

• Paradoxically, to write a recursive function, you must assume that the function is fully functional before you finish writing it; this is called the recursive leap of faith.
• Consider how you can solve the current problem using the solution to a simpler version of the problem. The amount of work done in a recursive function can be deceptively little: remember to take the leap of faith and trust the recursion to solve the slightly smaller problem without worrying about how.
• Think about what the answer would be in the simplest possible case(s). These will be your base cases - the stopping points for your recursive calls. Make sure to consider the possibility that you’re missing base cases (this is a common way recursive solutions fail).
• It may help to write an iterative version first.

Tree Recursion

A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.

For example, let’s say we want to recursively calculate the nth Virahanka-Fibonacci number, defined as:

def virfib(n):
    if n == 0 or n == 1:
        return n
    return virfib(n - 1) + virfib(n - 2)

Calling virfib(6) results in the following call structure that looks like an upside-down tree (where f is virfib):

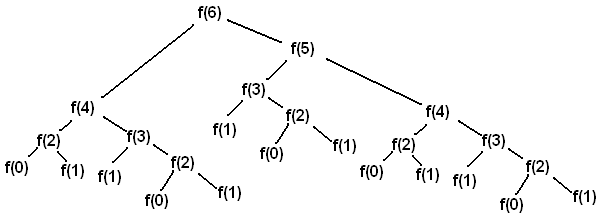
Each f(i) node represents a recursive call to virfib. Each recursive call f(i) makes another two recursive calls, which are to f(i-1) and f(i-2). Whenever we reach a f(0) or f(1) node, we can directly return 0 or 1 rather than making more recursive calls, since these are our base cases.

In other words, base cases have the information needed to return an answer directly, without depending upon results from other recursive calls. Once we’ve reached a base case, we can then begin returning back from the recursive calls that led us to the base case in the first place.

Generally, tree recursion can be effective for problems where there are multiple possibilities or choices at a current state. In these types of problems, you make a recursive call for each choice or for a group of choices.

Required Questions

What Would Python Do?

Q1: Squared Virahanka Fibonacci

Use Ok to test your knowledge with the following “What Would Python Display?” questions:

python3 ok -q squared-virfib-wwpd -u

Hint: If you are stuck, try drawing out the recursive call tree. See 02/11’s Lecture (Tree Recursion) for more information.

>>> def virfib_sq(n):
>>>     print(n)
>>>     if n <= 1:
>>>         return n
>>>     return (virfib_sq(n - 1) + virfib_sq(n - 2)) ** 2
>>> r0 = virfib_sq(0)
______

>>> r1 = virfib_sq(1)
______

>>> r2 = virfib_sq(2)
______

>>> r3 = virfib_sq(3)
______

>>> r3
______

>>> (r1 + r2) ** 2
______

>>> r4 = virfib_sq(4)
______

>>> r4
______

Parsons Problems

To work on these problems, open the Parsons editor:

python3 parsons

Q2: Line Stepper

Complete the function line_stepper, which returns the number of ways there are to go from start to 0 on the number line by taking exactly k steps along the number line. Note that at each step, you must travel either left or right; you may not stay in place!

For example, here is a visualization of all possible paths if we start at 3 on the number line with 5 steps. At every step, we move either one step to the left of right, and we ultimately end each path at 0.

def line_stepper(start, k):
    """
    Complete the function line_stepper, which returns the number of ways there are to go from
    start to 0 on the number line by taking exactly k steps along the number line.

    >>> line_stepper(1, 1)
    1
    >>> line_stepper(0, 2)
    2
    >>> line_stepper(-3, 3)
    1
    >>> line_stepper(3, 5)
    5
    """
    "*** YOUR CODE HERE ***"

Code Writing Questions

Q3: Summation

Write a recursive implementation of summation, which takes a positive integer n and a function term. It applies term to every number from 1 to n including n and returns the sum.

Important: Use recursion; the tests will fail if you use any loops (for, while).

def summation(n, term):
    """Return the sum of numbers 1 through n (including n) wíth term applied to each number.
    Implement using recursion!

    >>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
    225
    >>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
    54
    >>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
    62
    >>> # Do not use while/for loops!
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'summation',
    ...       ['While', 'For'])
    True
    """
    assert n >= 1
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q summation

Q4: Insect Combinatorics

Consider an insect in an M by N grid. The insect starts at the bottom left corner, (1, 1), and wants to end up at the top right corner, (M, N). The insect is only capable of moving right or up. Write a function paths that takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)

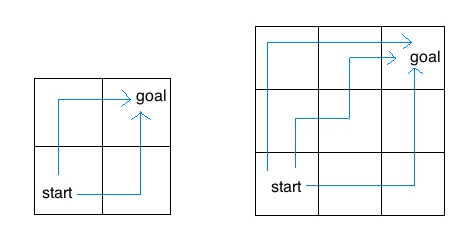
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).

Hint: What happens if we hit the top or rightmost edge?

def paths(m, n):
    """Return the number of paths from one corner of an
    M by N grid to the opposite corner.

    >>> paths(2, 2)
    2
    >>> paths(5, 7)
    210
    >>> paths(117, 1)
    1
    >>> paths(1, 157)
    1
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q paths

Submit

Make sure to submit this assignment by running:

python3 ok --submit

Optional Questions

Q5: Pascal’s Triangle

Pascal’s triangle gives the coefficients of a binomial expansion; if you expand the expression (a + b) ** n, all coefficients will be found on the nth row of the triangle, and the coefficient of the ith term will be at the ith column.

Here’s a part of the Pascal’s trangle:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

Every number in Pascal’s triangle is defined as the sum of the item above it and the item above and to the left of it. Rows and columns are zero-indexed; that is, the first row is row 0 instead of 1 and the first column is column 0 instead of column 1. For example, the item at row 2, column 1 in Pascal’s triangle is 2.

Now, define the procedure pascal(row, column) which takes a row and a column, and finds the value of the item at that position in Pascal’s triangle. Note that Pascal’s triangle is only defined at certain areas; use 0 if the item does not exist. For the purposes of this question, you may also assume that row >= 0 and column >= 0.

def pascal(row, column):
    """Returns the value of the item in Pascal's Triangle
    whose position is specified by row and column.
    >>> pascal(0, 0)
    1
    >>> pascal(0, 5)	# Empty entry; outside of Pascal's Triangle
    0
    >>> pascal(3, 2)	# Row 3 (1 3 3 1), Column 2
    3
    >>> pascal(4, 2)     # Row 4 (1 4 6 4 1), Column 2
    6
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q pascal